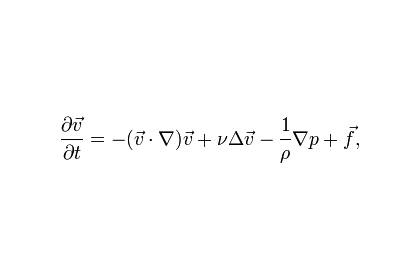Лауреат Филдсовской медали математик Теренс Тао опубликовал работу, которая доказывает невозможность решения посвященной задаче Навье-Стокса проблемы тысячелетия существующими на настоящий момент средствами. Препринт (pdf) статьи доступен на arXiv.org.
Тао попытался формализовать представление многих математиков о том, что существующая аналитическая техника недостаточна для решения знаменитой задачи. Для этого он построил пример уравнения, которое несколько отличается от задачи Навье-Стокса, но по большинству параметров (которые до последнего считались важными) с ней схожа. При этом полученная система обладает очень плохим с точки зрения математики свойством: в некоторых точках решения за конечное время достигают бесконечных значений.
Свои результаты Тао получил на основе работ математиков Нетца Каца и Наташи Павлович 2004 года для упрощенной системы Навье-Стокса. Они предложили такую схему: количество энергии в ограниченном объеме потока не изменяется, а сам объем уменьшается. Это и приводит к возникновению бесконечностей.
В новой работе Тао также представил программу - серию проблем - выполнение которой позволит теоретически получить нужные инструменты для решения задачи Навье-Стокса.
Уравнения Навье-Стокса - это система дифференциальных уравнений в частных производных, описывающих движение вязкой ньютоновской жидкости. Они используются в математическом моделировании многих прикладных задач физики. В частности, считается, что они описывают многие типы турбулентных потоков в динамике газа и жидкости.
Вопрос существования и единственности решений - одна из семи так называемых задач тысячелетия, за решение каждой из которых математический институт Клэя предлагает награду в миллион долларов (одна из задач - доказательство гипотезы Пуанкаре - была решена Григорием Перельманом, но он отказался от награды).
В середине января 2014 года казахстанский математик Мухтарбай Отелбаев заявил о решении задачи Навье-Стокса: ему якобы удалось доказать существование и единственность так называемых «сильных» решений. В настоящее время в работе Отелбаева уже были обнаружены серьезные пробелы.